Spatial resolution, noise and information in the computational-imaging era

Abstract

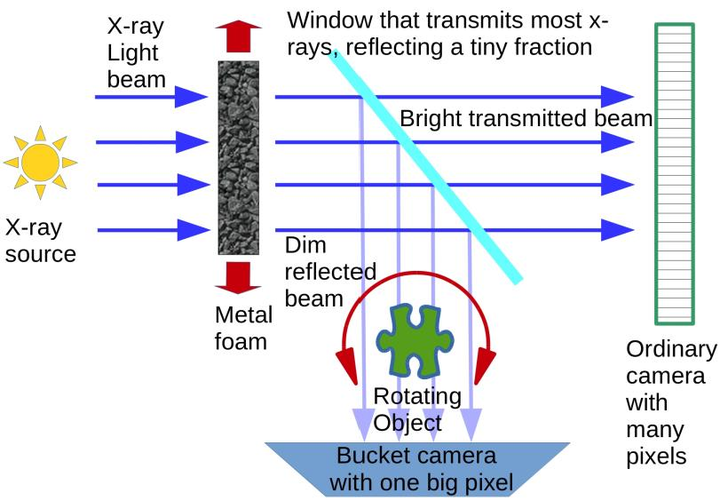
Imaging is an important means by which information is gathered regarding the physical world. Spatial resolution and signal-to-noise ratio are underpinning concepts. There is a paucity of rigorous definitions for these quantities, which are general enough to be useful in a broad range of imaging problems, while being also sufficiently specific to enable precise quantitative evaluation of the relevant properties of imaging systems. This is particularly true for many modern forms of imaging that include digital processing of the acquired imaging data as an integral step leading to final images presented to an end-user. Here, both the well-known historical definitions of spatial resolution and some more recent approaches suitable for many forms of modern computational imaging are discussed. An intrinsic duality of spatial resolution and signal-to-noise exists in almost all types of imaging, with the related uncertainty relationship determining a trade-off between the two quantities. Examples are presented with applications to super-resolution imaging, inline holography and ghost imaging.